Mô tả bài toán: cho đồ thị vô hướng G=(V,E) hãy xác định mọi đường đi từ đỉnh xuất phát đi qua tất cả các đỉnh mỗi đỉnh chỉ qua duy nhất 1 lần.
Ý tưởng thuật toán: sử dụng kỹ thuật tìm kiếm theo chiều sâu bằng cách đánh dấu đỉnh đã đi qua trong quá trình tìm kiếm.
Mô tả dữ liệu đầu vào và đầu ra của bài toán:
Dữ liệu vào: cho trong tập tin Bai4.inp
-  Dòng đầu ghi số n là số đỉnh của một đồ thị (0<n<100)
-  Dòng 2 ghi đỉnh xuất phát.
-  Dòng i+2 (1<=i<=n) chứa n số A[i,1], A[i,2],…, A[i,n] mỗi số cách nhau bởi một khoảng trắng.
Dữ liệu ra: in ra màn hình đường đi qua tất cả các đỉnh (nếu có).

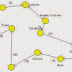
Ví dụ:

Cài đặt chương trình:
#include <stdio.h>
#include <conio.h>
#include <iostream.h>
#define FileIn "Bai4.inp"
intDem = 0;     
int *L;      
char  *DanhDau;  
int**A,n,D;
//Đọc dữ liệu từ tập tin theo yêu cầu bài toán
void Doc_File() {
FILE*f = fopen(FileIn,"rb");
fscanf(f,"%d%d",&n,&D);
cout<<"Ma Tran Lien Ket Tuong Ung.\n"<<D<<endl;
*A = new int [n];
for(int i =0;i<n;i++) {
A[i] = new int [n];
for(int j =0;j<n;j++) {
fscanf(f,"%d",&A[i][j]);
cout<<A[i][j]<<" ";
}
cout<<endl;
}
fclose(f);
D--;
}
//Khởi tạo dữ liệu ban đầu cho bài toán
void KhoiTao() {
DanhDau = new char [n];
L = new int [n];
for (int i = 0; i<n; i++) {
DanhDau[i] =0;  
L[i] = 0;
}
DanhDau[D] = 1;    
L[0] = D;
}
//Xuất đường đi ra màn hình
void InDuongDi(int Dinh) {
Dem++;
cout<<endl<<D+1;
for (int i = 1; i<Dinh; i++)
cout<<" -> "<<L[i]+1;
}
//Tìm kiếm đường đi
void Try(int Dinh){
if(Dinh == n) 
InDuongDi(Dinh);
else {
for(int i = 0; i<n; i++)
if( A[L[Dinh-1]][i]>0 && DanhDau[i] == 0){
L[Dinh] = i;
DanhDau[i] = 1;  
Try(Dinh+1);   
L[Dinh] = 0;
DanhDau[i] = 0; 
}
}
}
//Chương trình chính
void main() {
clrscr();
Doc_File();
KhoiTao();
cout<<"Duong di";
Try(1);
if(Dem==0)
cout<<" khong co.";
delete*A,DanhDau,L;
getch();

}
Kết quả chạy chương trình:

Tags: Kỹ thuật lập trình, c, c++, pascal, java, đồ thị, hamilton, tìm đường đi